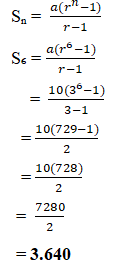Nama : Kelpin
Dwi Amanda
NIM : 01010582024138
Kelas :
1A6 D3 Akuntansi Universitas Sriwijaya
SOAL:
Lanjutkan : Kerjakan Soal Latihan di bawah ini;
1.
Jika
S3 dan S7 dari sebuah
deret hitung masing-masing adalah 50 dan 70,
Hitunglah :
a.
S10,
b.
dan
D5.
Dijawab :
a. S10…..?
I) Sn
= a + ( n - 1) b II) Sn = a + (n - 1
) b
S3 = a + ( 3-1 ) b
S7
=a + ( 7-1 ) b
50 = a + 2b
70 = a + 6b
Menggunakan cara Eliminasi :
50 = a + 2b x6
70 = a + 6b x2
300= 6a + 12b
140= 2a + 12b
160=4a
160=a
4
40 =a / S1
S10 = a + (n - 1) b
= 40 + (10 - 1) 5
= 40 + (9) × 5
= 40 + 45 = 85
b.D5………..?
S5 = a + ( n – 1 ) b
= 40 + ( 5 – 1 ) 5
= 40 + 20
= 60
D5 = ½ n ( a + S5 )
= ½ 5 ( 40 + 60 )
= 2,5 ( 100 )
D5 = 25
2.
Apabila
Suku ke 3 dan ke 7 dari suatu Deret Ukur Masing – Masing adalah 800 dan 204.000
berapa :
a.
a……?
b.
p……?
c.
S5………?
d.
J5………?
Jawab :
a.
Dik :
U3 = 800
U7 = 204.000
Dit : a……….?
Dij :
a. p² = 800
a . p⁶ = 204.000
U7 : U3 = 204.000 : 800
(a . p⁶) : (a . p²) = 255
p⁴ = 255
p = 4
a . p² = 800
a . 4² = 800
a . 16 = 800
a = 800 : 16
a = 50
b.
P
= 4
c.
S5……….?
Jawab :
S5 = a(p⁵ - 1) / p – 1
= 50(4⁵ - 1) / 4 – 1
=
(50 x 1023) / 3
= 17050
d.
J5 = ½ n ( a + S5 )
= ½ 5 ( 50 + 17050 )
= 2,5 ( 17100 )
= 42750
Soal Latihan :
8. Perluas Persamaan Berikut Ini :
( X
– 5 ) (4X – 5 ) = ….
Jawab :
( X
– 5 ) ( 4X – 5 ) = X ( 4X – 5 ) – 5 ( 4X – 5 )
= 4X2 – 5X – 20X + 25
= 4X2 – 25X + 25
9. 4X – 18Y = 6
2X –
5Y = -1
carilah nilai x dan y
Jawab
:
·
Eliminasi persamaan
4X
– 18Y = 6 I 2 I 8x – 36y = 12
2X
– 5Y = -1 I 4 I 8x – 20y = -4
-16y
= 16
y
= 16
-16
y = -1
·
Subtitusikan
4x
-18y = 6
4x
– 18 (-1) = 6
4x + 18 = 6
4x = 6 – 18
4x = -12
x = -3
Jadi,
nilai x = -3 dan y = -1
10. 3x + 2y – 5z = -12
2x + 3y
+ 4z = -17
X – 5y +
3z = -3 carilah
nilai x,y,z …
Jawab
:
Dik
:
3x + 2y – 5z = -12 = persamaan 1
2x + 3y + 4z = -17 = Persamaan 2
X – 5y + 3z = -3 = Persamaan 3
Penyelesaian
:
Eliminasi persamaan 1
dan persamaan 2
3x + 2y – 5z = -12 I 3
I 9x + 6y – 15z = -36
2x + 3y + 4z = -17 I 2 I 4x + 6y +
9z = -34
5x – 23z = -2 ( Persamaan 4 )
Eliminasi
Persamaan 2 dan 3
2x
+ 3y + 4z = -17 I 5 I 10x + 15y + 20z = -85
X –
5y + 3z = -3 I 3 I 3x – 15y + 9z = -9
13x + 29z = - 94 ( Persamaan 5 )
Eliminasi persamaan 4
dan 5
5x + 23z = -2 I 13
I 65x – 299z = -26
13x + 29z = -94 I 5 I
65x + 145z = -470
-444z = 444
Z = -1
Subtitusikan :
5x – 23z = -2
5x – 23 (-1) = -2
5x + 23 = -2
5x
= -2 – 23
5x = -25
X = -5
Subtitusikan nilai x =5 dan z = -1
x-5y+3z = -3
-5 -5y + 3(-1) = -3
-5 – 5y -3 = -3
-5y = -3 + 8
-5y = 5
Y = -1
Lanjutkan : Kerjakan Soal Latihan di bawah ini;
1.
Jika
S3 dan S7 dari sebuah
deret hitung masing-masing adalah 50 dan 70,
Hitunglah :
a.
S1,
b.
S10, dan D5.
Dijawab :
a. S1…..?
I) Sn
= a + ( n - 1) b II) Sn = a + (n - 1
) b
S3 = a + ( 3-1 ) b
S7
=a + ( 7-1 ) b
50 = a + 2b
70 = a + 6b
Menggunakan cara Eliminasi :
50 = a + 2b x6
70 = a + 6b x2
300= 6a + 12b
140= 2a + 12b
160=4a
160=a
4
40 =a / S1
B. S10 & D5……?
S10 = a + (n - 1) b
= 40 + (10 - 1) 5
= 40 + (9) × 5
= 40 + 45 = 85
S5 = a + ( n – 1 ) b
= 40 + ( 5 – 1 ) 5
= 40 + 20
= 60
D5 = ½ n ( a + S5 )
= ½ 5 ( 40 + 60 )
= 2,5 ( 100 )
D5 = 25
2.
Suatu
Deret Ukur yang suku-sukunya 10,30,90,270,..........,
Hitunglah
;
a. S6,
b.
S10,
c.
D6, dan
d.
D10.
a. S6….?
r = Uₙ/ Uₙ₋₁
r = U₂ / U₁
r = 30 / 10
r = 3
b. S10….?
c. D6……….?
D6 = ½ n
( a + s6 )
= ½ 6 ( 10 + 3640)
= 3 ( 3740 )
= 11.220
d. D10……?
D10 = ½
n ( a + s10)
= ½ 10 ( 10 + 295.240 )
= 5 (
295.250 )
= 1.476.250
Jadi nilai x = -5,y=-1 dan z = -1